This site uses cookies. By continuing to browse the site, you are agreeing to our use of cookies. Privacy Policy
Okay, thanksOption pricing is sometimes described as “multi-dimensional,” meaning a variety of factors simultaneously influence the price of an option. These factors are referred to as “the Greeks” and are named using letters of the Greek alphabet- delta, theta, rho, gamma, and vega. Understanding all of “the Greeks” is important in understanding how the price of an option or option strategy might fluctuate. In this post we will focus on delta.
The Greek letter “P,” pronounced ‘rōw’.
One of the more hotly debated topics is exactly when and how much the Federal Reserve will be raising interest rates in the near future. It finally appears a credible plan of systematic interest rate raises is in place.
However, market conditions can still have an impact on whether or not the Federal Reserve ultimately acts or remains “data dependent.” After many years of essentially zero rates, it was inevitable that rates should finally move higher.
This is a good opportunity to review how option prices are affected by changes in interest rates (Rho) and what that means.
Federal Reserve Interest Rate Probability

In general, of the five basic inputs used to price options (Delta, Theta, Vega, Gamma, and Rho), interest rates are of the least concern. This is because most option strategies are short-term in nature, and changes in interest rates will have very little impact.
In contrast, option strategies that have longer maturities, such as Long-Term Equity Anticipation Securities (LEAPS), can have a significant impact on option pricing. Once again, Rho risk gets little respect since most traders employ short term strategies; thus there is little impact on option prices with changes in interest rates. However, there can be material changes to premiums with longer-dated options, so Rho risk should not be ignored.
There are cash flows involved in trading options that can result in either credits or debits. These cash flows will either earn interest or be charged a borrowing fee. Therefore, interest rates must be considered as one of the basic inputs that go into the generally accepted Black-Scholes option pricing model.
Interest rates affect the forward price of a given underlying.
For our example, we will use stock-type settlement.
Option pricing models assume delta neutrality.
Let’s explain this by using put-call parity, which assumes identical pay-off structures can be replicated various ways with options.
Under the assumption of parity, there are no arbitrage opportunities.
If interest rates decline, the holder of long stock will be paying less in borrowing costs and should be willing to sell the call at a cheaper price and purchase the put at a higher price to hedge the position.
If short stock is held and interest rates rise, then the short stock rebate collected will increase and the short stock holder should be willing to purchase the call at a higher price and sell the put at a lower price to hedge the position.
In other words, if one does not account for Rho, a clever trader would be able to earn a riskless, arbitrage profit.
Typically, the risk-free rate is the rate used in the option pricing model to derive theoretical prices. Yields on government securities with maturities equivalent to the expiry of the option would be the appropriate input into the model. In reality, however, we cannot lend and borrow at the same government rate so a more realistic, or “tradable,” rate may be the yield on Eurodollar futures, for example.
Complicating matters even more, most traders must borrow at a higher rate and lend at a lower rate, so their models might even incorporate multiple rates like required when evaluating options on foreign currencies.
In short, Rho is positive for calls and negative for puts.
As discussed, the Rho is much greater for longer term options. Rho increases as calls go further in the money and decreases (gets more negative) as puts go further in the money.
Below are two graphs demonstrating the Rho characteristics for calls and puts. In the call example, the stock price is at $2120. Strikes range from 1000 up to 3500 and the time until expiration ranges from 0 out to 720 days. The graph clearly shows that deeper in the money calls (strikes less than the current stock price and with more time to maturity) have the most sensitivity to changes in interest rates.
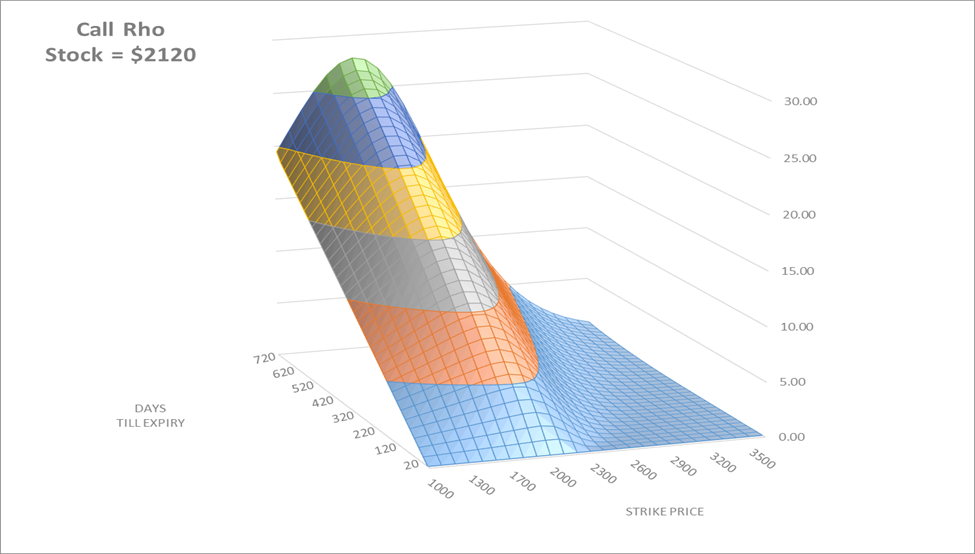
Source: Swan Global Investments
The same can be said for puts, except now higher strikes with more time until expiration will have the most sensitivity to changes in interest rates.
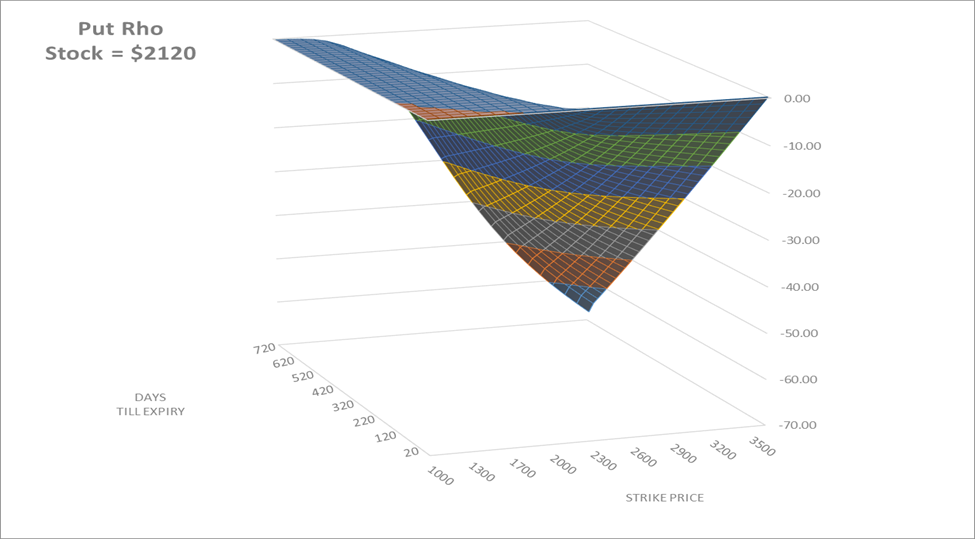
Source: Swan Global Investments
Those who utilize option strategies must always be cognizant of all the potential risks. No option in any strategy is “perfect.” There is always a trade-off between the potential factors that can alter an option’s value. Suffice it to say, even though options with longer-term maturities do have more exposure to changes in interest rates, this risk is off-set by lower decay costs and more stability with respect to volatility than shorter-term options. Rising interest rates actually decreases the cost of put calendar spreads, so it is possible that losses suffered as a result of a rising interest rate environment in the short-term, may be offset in the future when it is time to roll puts by purchasing a “cheaper” spread.
Over the last few years with short-term rates held close to zero, Rho risk has essentially been a non-issue. This will likely change moving forward as we are about to begin a new interest rate cycle that many have not witnessed or simply forgot what it felt like.
Consequently, adhering to sound risk management principles and proper assessment of all risks will help navigate you in merrily achieving your financial goals.
Check out the rest of the Greek Lessons blog series:
Feel free to review more information on the Defined Risk Strategy performance, or its components, or call 970.382.8901.
This post continues the ‘Where the DRS Fits’ series, exploring how the Swan DRS can serve as a total portfolio solution, as designed by founder Randy Swan.
NEXT ARTICLEChris Hausman, CMT®, Portfolio Manager, Managing Director-Risk, focuses on risk assessment and management for the Defined Risk Strategy investments and positions. He monitors risk across all of Swan’s portfolios and prepares stress tests, risk assessment reports and contributes to strategic decision making for the investment management team, as well as serving as an additional layer of oversight for the trading team. As a Chartered Market Technician, he also acts as Chief Technical Strategist at Swan Global Investments.
Swan Global Investments, LLC is a SEC registered Investment Advisor that specializes in managing money using the proprietary Defined Risk Strategy (“DRS”). SEC registration does not denote any special training or qualification conferred by the SEC. Swan offers and manages the DRS for investors including individuals, institutions and other investment advisor firms. Any historical numbers, awards and recognitions presented are based on the performance of a (GIPS®) composite, Swan’s DRS Select Composite, which includes non-qualified discretionary accounts invested in since inception, July 1997, and are net of fees and expenses. Swan claims compliance with the Global Investment Performance Standards (GIPS®). All data used herein; including the statistical information, verification and performance reports are available upon request. The S&P 500 Index is a market cap weighted index of 500 widely held stocks often used as a proxy for the overall U.S. equity market. Indexes are unmanaged and have no fees or expenses. An investment cannot be made directly in an index. Swan’s investments may consist of securities which vary significantly from those in the benchmark indexes listed above and performance calculation methods may not be entirely comparable. Accordingly, comparing results shown to those of such indexes may be of limited use. The adviser’s dependence on its DRS process and judgments about the attractiveness, value and potential appreciation of particular ETFs and options in which the adviser invests or writes may prove to be incorrect and may not produce the desired results. There is no guarantee any investment or the DRS will meet its objectives. All investments involve the risk of potential investment losses as well as the potential for investment gains. Prior performance is not a guarantee of future results and there can be no assurance, and investors should not assume, that future performance will be comparable to past performance. All investment strategies have the potential for profit or loss. Further information is available upon request by contacting the company directly at 970–382-8901 orwww.www.swanglobalinvestments.com. . 088-SGI-041317