This site uses cookies. By continuing to browse the site, you are agreeing to our use of cookies. Privacy Policy
Okay, thanksThere is a common the phrase, ‘some things in life are all about timing’. In regard to options contracts, timing is an extremely important variable in determining price or value of the contracts.
Theta, in options vernacular, refers to the degenerative impact of time on the price of an option contract. An option contract offers the buyer the right, but not the obligation, to buy (call) or sell (put) a security or other financial asset at an agreed-upon price (the strike price) during a certain period of time or on a specific date (exercise date).
How does one value such an instrument? The answer involves the concept of time decay.
Fischer Black, Myron Scholes, and Robert Merton answered this question in the early 1970’s with the famous Black-Scholes option pricing model. Without going into the gory details, the model says several inputs are necessary to value an option, including the current price of the asset, the volatility of the asset’s price, the agreed upon price that the asset can be bought or sold, and the time frame over which the option is valid.
That last variable, the time value of the option, is worth exploring in more detail. The closer the expiration date, the lower the time value is of the option. This is known as “time decay” or “theta decay”. An important feature of time decay is that it does not happen in a straight line. Time decay starts off slow and then accelerates as the expiration date draws near. The graph below illustrates the notion of time decay.
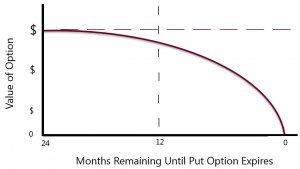
Anyone who ever bought a ticket from a scalper to a sporting event should be familiar with this phenomenon. The ticket is like an option; it is an option to attend the event. However, as soon as the game is over the ticket is worthless. If the big game is a month or two away the scalper’s price will fluctuate a bit depending upon the demand for tickets. But if the demand for seats isn’t there, the price of that ticket starts to drop in the days and hours leading up to kick-off. The scalper doesn’t want to be left holding a bunch of unsold tickets (i.e., expired options), so a ticket selling for $200 a month ago might be had for $10 just before the game starts. This is an example of time decay.
A key component of Swan’s Defined Risk Strategy (DRS) is to actively manage time decay. Swan purchases long-term two-year put options to help protect its market holdings against downturns. Hence the name, defined risk strategy.
During the first year, the market position has protection while the put option is exposed to a small amount of time decay. The DRS then avoids the second half of the above chart by selling off the option in the secondary market about a year before expiration.
Then, the hedge is re-established by purchasing a new two-year LEAP. By engaging in this “rolling hedge” strategy, the DRS is not left holding a bunch of worthless, expired put contracts at the end of the year.
This is a much more efficient, cost-effective way of Protecting a Portfolio Against Systematic Risk and is rather unique to Swan’s DRS.
Serving Up Diversification For decades the financial industry has promoted diversification as the most logical, prudent way to maximize returns and minimize risk. However, in order to truly reap the benefits of diversification, a strategic […]
NEXT ARTICLEMarc Odo, CFA®, CAIA®, CIPM®, CFP®, Client Portfolio Manager, is responsible for helping clients and prospects gain a detailed understanding of Swan’s Defined Risk Strategy, including how it fits into an overall investment strategy. Formerly Marc was the Director of Research for 11 years at Zephyr Associates.
Swan Global Investments, LLC is a SEC registered Investment Advisor that specializes in managing money using the proprietary Defined Risk Strategy (“DRS”). SEC registration does not denote any special training or qualification conferred by the SEC. Swan offers and manages the DRS for investors including individuals, institutions and other investment advisor firms. Any historical numbers, awards and recognitions presented are based on the performance of a (GIPS®) composite, Swan’s DRS Select Composite, which includes non-qualified discretionary accounts invested in since inception, July 1997, and are net of fees and expenses. Swan claims compliance with the Global Investment Performance Standards (GIPS®). All data used herein; including the statistical information, verification and performance reports are available upon request. The S&P 500 Index is a market cap weighted index of 500 widely held stocks often used as a proxy for the overall U.S. equity market. Indexes are unmanaged and have no fees or expenses. An investment cannot be made directly in an index. Swan’s investments may consist of securities which vary significantly from those in the benchmark indexes listed above and performance calculation methods may not be entirely comparable. Accordingly, comparing results shown to those of such indexes may be of limited use. The adviser’s dependence on its DRS process and judgments about the attractiveness, value and potential appreciation of particular ETFs and options in which the adviser invests or writes may prove to be incorrect and may not produce the desired results. There is no guarantee any investment or the DRS will meet its objectives. All investments involve the risk of potential investment losses as well as the potential for investment gains. Prior performance is not a guarantee of future results and there can be no assurance, and investors should not assume, that future performance will be comparable to past performance. All investment strategies have the potential for profit or loss. Further information is available upon request by contacting the company directly at 970–382-8901 orwww.www.swanglobalinvestments.com. 021-SGI-052815