Put-Call Parity

Long or short options have positive or negative Gammas whether they are calls or puts. Remember that option pricing models assume Delta neutrality, which assumes identical pay-off structures can be replicated various ways with options. It is possible to construct synthetic long underlying by purchasing a call and selling a put on the same underlying with the same strike and expiration.

We know that the Delta of underlying is always 100; therefore, the Delta of synthetic stock (long call and short put) should always be 100 as well.

In our previous example, the June 100 call had a Gamma of 10 and the Delta increased from 50 to 60 as the stock rose $1. The put will have the same Gamma as the call and its Delta will also move by 10. The trick with puts, however, is that they have negative Deltas. So, the June 100 put, which also started out as an at the money option with a -50 Delta, moves from -50 to -40. This is a positive increase in Delta. If we apply the synthetic stock check, we see that the new call Delta (+60) plus the Delta of the short put (+40) adds up to +100 Deltas.

In summary, the Gammas of puts and calls on the same underlying, expiration, and strike will equal each other as a result of put-call parity.

Now let’s look at what strikes have the most Gamma within the same expiration.

At the Money Options and Gamma

As a general rule, the at the money strike will have the most Gamma within an expiration. The change in Delta will be most pronounced as an option moves from being at the money to either in or out of the money.

By examining an extreme example, we can imbed the concept of an at the money option having the most Gamma.

Let’s say an at the money option is seconds from expiring. The option pricing model will still show the option as having a 50 Delta. If the underlying moves up and the option expires, a call option will now have a 100 Delta and the corresponding put will have a 0 Delta. This is quite a large move in the Delta and thus shows how at the money options have the most Gamma.

For another way to understand what Gamma is like, let us turn to an analogy.

Say, for example, you have two basketball teams, maybe North Carolina and Villanova. When are changes to the score most important? Obviously, in a close game with only a few seconds left on the clock. If the score is Villanova 74, North Carolina 71 with only 6.7 seconds left, ANY change in the variables matter, but a made three pointer will change the complexion of the game entirely. This is the “high Gamma” part of the game. If the score is tight, that is like having a near- or at-the-money option where small moves in price will determine whether that option is a winner (in the money) or loser (out of the money).

Out of the Money Options and Gamma

What about strikes that are further away from the underlying price? Well, as expiration approaches, out of the money options are approaching 0 Delta and in the money options are approaching 100 Delta, so their Delta will not move as much as the Delta of an at the money option. Thus, when Gamma is small in absolute terms, Delta changes slowly with changes in the underlying asset price. However, if Gamma is large in absolute terms, Delta is highly sensitive to the changes in the underlying asset price.

Using our previous example of a basketball game, imagine a situation where we are only five minutes into the first half of the game or maybe a game that is a blowout. A bucket is still worth two or three points, but its impact on the final outcome is much less important. Changes to the score aren’t as important in those situations. Along those same lines, if there is a lot of time left to expiration, or if the option is deep in or out of the money, Gamma is lower.

Time and Gamma

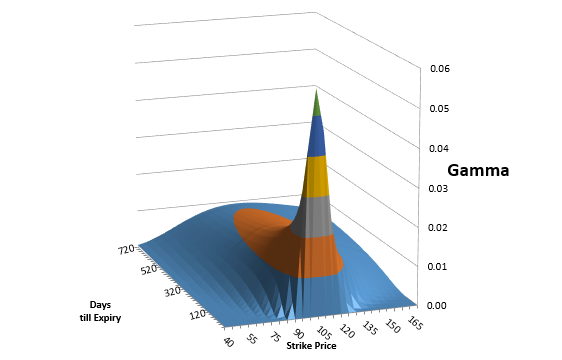
With respect to time, shorter term options will have more Gamma than longer term options. Referring to our expiration example, an option with more time will not have such a pronounced Delta change as one that is expiring sooner. The chart below illustrates both Gammas with respect to time and strike location. Options with more time until expiration have smoother Gammas, with the at the money strike (at the money = 100) still having the most Gamma within a given expiration. One can clearly see how the Gamma increases greatly as expiration approaches, again, with the at the money strike still having the most Gamma than surrounding strikes.

Conclusion

Even though Gamma does not directly measure changes in option values for changes in underlying prices, it is still an important risk measurement.

It signifies the potential changes in option premium as measured by Delta. Many option premium strategies are short term in nature, and as a result, these strategies take on a tremendous amount of Gamma risk.

Premium selling strategies that appear Delta-neutral may have hidden risks such as Deltas moving around as options approach expiration or the potential for certain types of spreads to produce an inordinate number of Deltas under certain market conditions.

One of the benefits of short premium strategies is the collection of Theta, or time decay; however, Gamma can quickly wipe out any Theta benefit if the underlying begins to move towards the short strike and the options approach expiration. A premium selling program must not only be concerned about maximizing Theta, but minimizing the effects of Gamma and the resulting Deltas on a portfolio.

A portfolio manager can never just focus on one type of risk but must juggle all of them to produce the most suitable risk-reward profile. Only a sound management process void of “blinders” can concurrently navigate all the risks while adding incremental returns to a portfolio in all market conditions.